La dinamica dell'innamoramento
Pubblicato il 11 gen 2026
“Un modello scientifico è una rappresentazione approssimata, fisica concettuale o matematica, di un fenomeno complesso, utilizzata come strumento logico per formulare congetture sui meccanismi interni e sul comportamento dei singoli elementi che lo compongono. Esso funge da ponte tra l’osservazione e la teoria, permettendo di spiegare e prevedere dinamiche non direttamente accessibili attraverso un processo iterativo di verifica e raffinamento.”
Un modello quindi è una rappresentazione approssimata.
Non è la realtà. È un tentativo.
Un ponte fragile tra ciò che osserviamo e ciò che proviamo a capire.
Serve a dare un ordine. O almeno l’illusione di un ordine.
Perché parto da qui?
Stavo scrivendo un post su questa conferenza del Professor Sergio Rinaldi, docente di teoria dei sistemi al Politecnico di Milano, dal titolo ”La dinamica dell’innamoramento“.
Mentre descrivevo il modello da lui proposto e le simulazioni associate, mi sono fermato.
Ma ha davvero senso modellizzare l’innamoramento?
Come scrivo anche nel post “L’amore”, “l’amore non si prevede, si vive.”
Allora che facciamo?
Abbracciamo il caos totale delle relazioni?
Oppure ha comunque senso modellizzare una scatola approssimativa di come ci innamoriamo?
E soprattutto.
Che cos’è davvero il caos?
Perché le relazioni con l’altro lo sono?
Troppe domande.
A cui però volevo rispondere.
E credo di essere arrivato ai confini dello scibile umano.
Quindi parliamone.
Tutto nasce dal fatto che siamo sistemi.
si Andrea l’abbiamo capito…! Lezione ricevuta.
Menomale dai…
Ma esserlo ha conseguenze profonde.
Come sistemi siamo deterministici ma imprevedibili.
Conosciamo il nostro istante iniziale ma non conosciamo il nostro istante finale.
Sappiamo solo che esiste.
Ma non conosciamo la traiettoria, che tipo di percorso si fa.
E più il sistema è giovane, complesso, sensibile, più diventa difficile prevedere dove andrà.
Essendo sistemi siamo fatti di elementi interconnessi.
E come tali un singolo pirulino può portare cambiamenti sistemici inaspettati.
Questo è quello che sapevo fino a poco fa.
Mi sono voluto spingere oltre.
Così sono arrivato alla Teoria del Caos.
Formalizzata per la prima volta da Edward Lorenz.
Un meteorologo.
Cercando di migliorare le previsioni del meteo, Lorenz scoprì qualcosa di sconcertante.
Esistono sistemi in cui la previsione a lungo termine è impossibile per natura.
Non perché il modello sia sbagliato.
Non perché manchino equazioni.
Ma perché non conosciamo mai davvero il presente.
Anche una minuscola approssimazione iniziale è sufficiente a far divergere completamente il risultato.
Tagli un decimale.
E il futuro cambia volto.
Lorenz lo sintetizza così:
“When the present determines the future but the approximate present does not approximately determine the future.”
Il presente determina il futuro.
Ma un presente approssimato non determina un futuro approssimato.
Due particelle partono quasi dallo stesso punto.
All’inizio sembrano inseparabili.
Poi qualcosa accade.
Una devia.
L’altra no.
E in poco tempo si ritrovano in regioni opposte dello spazio.
Una differenza invisibile ha creato due mondi diversi.
Eppure, se invece di seguire la singola traiettoria osserviamo l’intero sistema, emerge qualcosa di straordinario.
Tutte queste traiettorie caotiche non fuggono via.
Si intrecciano.
Si avvolgono.
Danzano attorno a una forma precisa.
Una forma che somiglia a una farfalla.
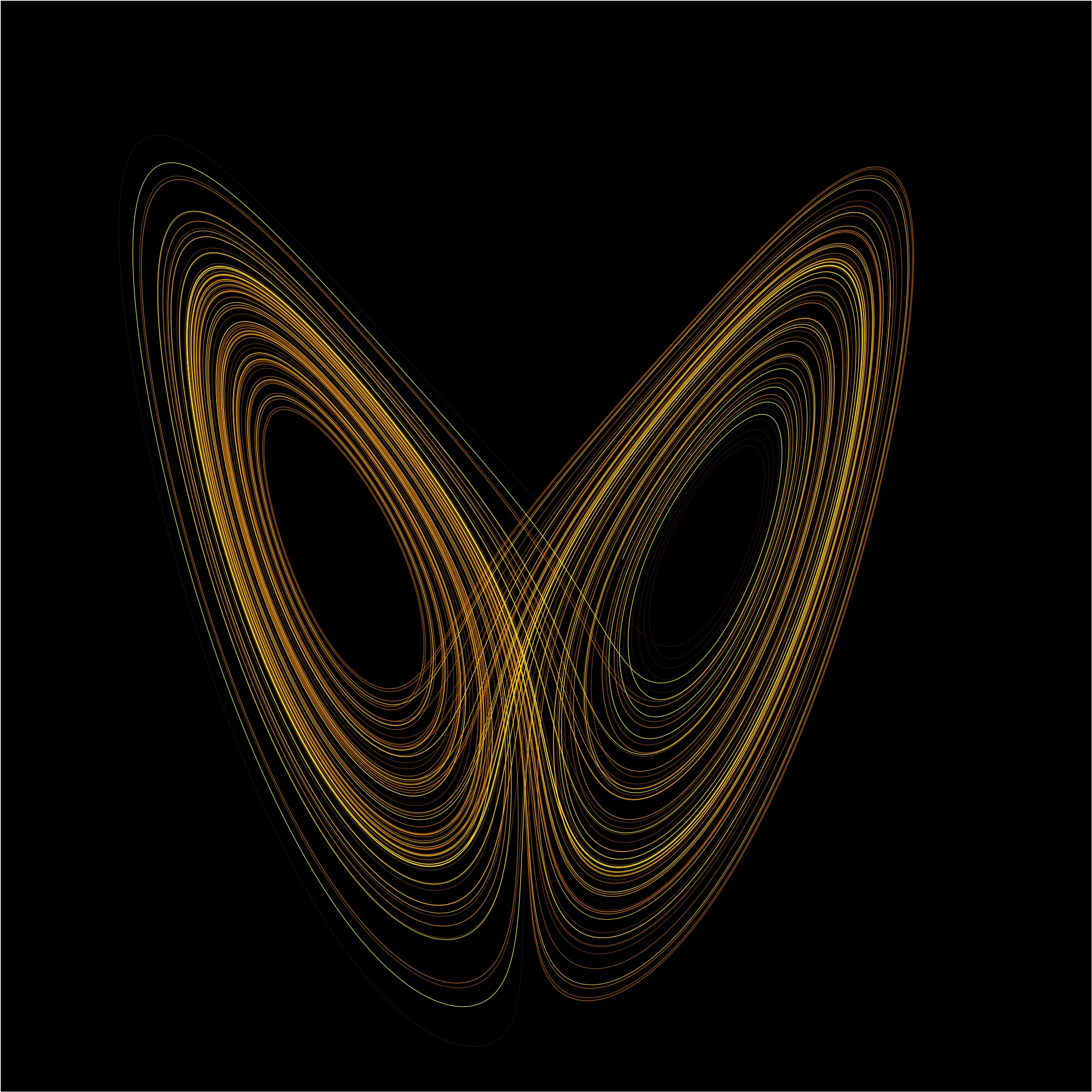
Si chiama Effetto Farfalla.
E ora il nome non sembra più una metafora poetica, ma una conseguenza geometrica.
Un’approssimazione minuscola, un decimale tagliato, un battito d’ali quasi impercettibile, può produrre un evento completamente diverso dall’altra parte del sistema.
Ma allora perché queste traiettorie non fuggono via?
Perché non si disperdono nello spazio infinito?
Perché lo spazio non è infinito.
È limitato.
Le traiettorie sono attratte da una struttura invisibile, una sorta di oggetto magnetico chiamato attrattore di Lorenz.
Non le guida lungo un percorso preciso.
Le costringe semplicemente a restare nella scatola.
Il movimento che ne nasce è continuo.
Stretching and folding.
Lo stretching fa sì che due punti inizialmente vicinissimi diventino imprevedibili.
Il folding impedisce loro di perdersi per sempre.
Si ripiegano su se stessi.
Rimangono confinati.
Da questa danza nasce una struttura complessa.
Un frattale.
Una forma di lunghezza infinita racchiusa in uno spazio finito.
Ed è proprio questa struttura.
La farfalla.
È l’attrattore di Lorenz.
Tolti i tecnicismi.
Questo cosa ci fa capire?
Ci fa capire che se segui la singola particella non saprai prevedere nulla.
Se osservi l’intero sistema, c’è un ordine profondo.
Sai dove può stare.
Sai dove non potrà mai arrivare.
Per questo i sistemi sono deterministici ma imprevedibili.
Deterministici perché conosciamo la loro forma.
Imprevedibili perché non ne conosciamo il possibile contenuto futuro.
“You can’t predict how any individual state will evolve, but you can say how a collection of states evolves. You must know the shape of the butterfly. ” dice il caro Veritasium.
Questo concetto di caos è alla base di numerosi aspetti della vita reale.
La finanza quantitativa.
La psicologia.
Il nostro stesso funzionamento.
Siamo caotici.
In senso fisico.
Non conosciamo davvero il nostro presente.
E quindi non possiamo prevedere il nostro futuro.
Possiamo individuare pattern.
Archetipi.
Comportamenti ricorrenti.
Ma ogni sistema resta unico.
E allora torno alla domanda iniziale.
Ha senso modellizzare la dinamica dell’innamoramento?
Probabilmente sì.
Non per prevedere.
Ma per delimitare.
Il modello del professor Rinaldi non è il cuore della questione.
Il cuore è il gesto.
Il tentativo di dare forma a qualcosa che sfugge.
In questa conferenza, che consiglio davvero di vedere, si tenta un’operazione audace.
Trovare un’equazione dell’innamoramento.

Il modello prova a fare previsioni partendo da dati raccolti da storie d’amore tratte dalla letteratura.
Il romanzo diventa il laboratorio.
La fine della storia, il punto di validazione.
E, sorprendentemente, spesso ci prende.
Il modello individua alcuni fattori ricorrenti. Non tutti, ovviamente. Ma quelli più diffusi.
Il fascino e l’amore restituito dal partner sembrano essere i due elementi principali.
Descrive come l’amore venga metabolizzato nel tempo.
Come tenda a diminuire nella crescita percentuale.
Come, dopo una fase iniziale, si stabilizzi.
Emergono anche due archetipi fondamentali: Il sicuro e l’insicuro.
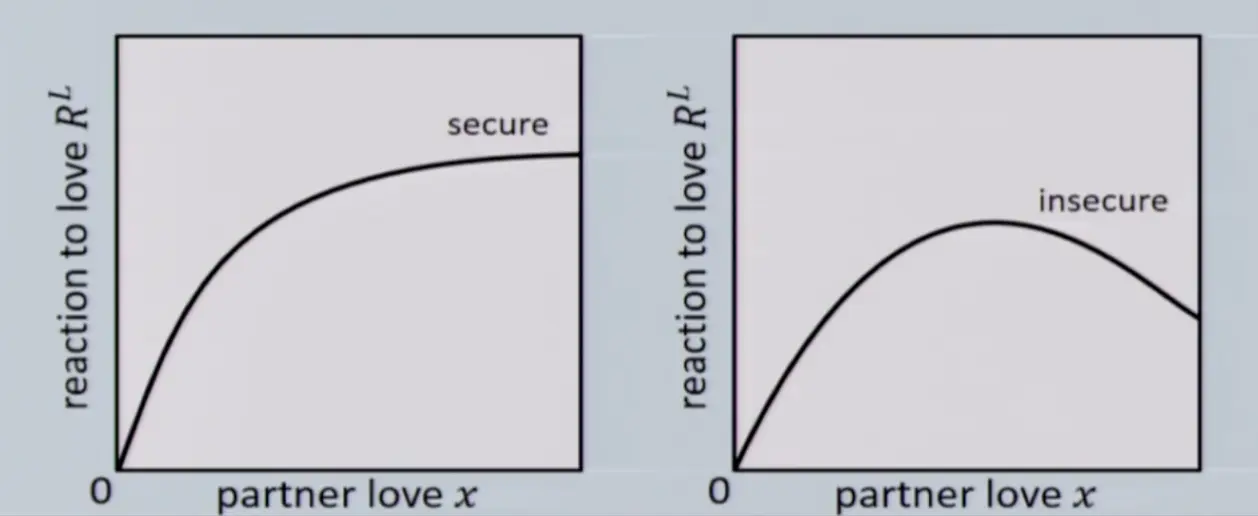
Nel primo caso, più il partner ama, più cresce la risposta all’amore.
Nel secondo accade il contrario: più il partner ama, meno aumenta la reazione.
Fino, a volte, a tendere all’abbandono.
Insicuro perché forse teme l’attaccamento.
Il declino fisiologico dell’amore. O semplicemente ciò che verrà dopo.
Il modello funziona? Spesso.
Ma non perché cattura l’amore.
Perché cattura il perimetro in cui l’amore si muove.
Resto però netto.
La matematica non potrà mai modellizzare le sottigliezze.
I sorrisi.
Gli sguardi.
Le incomprensioni.
I silenzi.
L’amore è qualcosa di talmente sottile.
Che anche conoscendone le equazioni, non arriveremmo nemmeno ad avvicinarci ad una previsione dell’1%.
Non esiste uno strumento che misuri quanto siamo innamorati.
Non esiste un presente conosciuto con precisione infinita.
E quindi l’amore resta imprevedibile.
Truffaut diceva che:
“l’amore è il risultato di due forze contrastanti, una forza di attrazione e l’altra di repulsione”.
Questa continua danza forse è l’unica certezza che abbiamo.
Possiamo solo sapere che alla fine lo spazio è limitato.
Il tempo pure.
Ed alla fine rimarremo ancorati a quell’orbita.
Finché non troveremo qualcuno con cui danzare.
Sempre mantenendo questa imprevedibilità.
Che forse è il bello della vita.
Noi esseri umani siamo gli unici animali che si pongono domande.
Cerchiamo modelli.
Spiegazioni.
Ordine.
E poi scopriamo che anche aumentando l’accuratezza dei nostri modelli all’infinito.
La vita resta imprevedibile.
Ma se osservi dall’alto.
Tutto ha senso.
Tutto è in ordine.
Chissà che disegno verrà fuori dalle nostre traiettorie?
A presto.
A.L.